这是一个基于 python 的基于收入预测支出的简单程序。

1
2
3
4
5
6
7
8
9
10
11
12
# 每月收入
x = [9558, 8835, 9313, 14990, 5564, 11227, 11806, 10242, 11999, 11630,
     6906, 13850, 7483, 8090, 9465, 9938, 11414, 3200, 10731, 19880,
     15500, 10343, 11100, 10020, 7587, 6120, 5386, 12038, 13360, 10885,
     17010, 9247, 13050, 6691, 7890, 9070, 16899, 8975, 8650, 9100,
     10990, 9184, 4811, 14890, 11313, 12547, 8300, 12400, 9853, 12890]
# 每月支出
y = [3171, 2183, 3091, 5928, 182, 4373, 5297, 3788, 5282, 4166,
     1674, 5045, 1617, 1707, 3096, 3407, 4674, 361, 3599, 6584,
     6356, 3859, 4519, 3352, 1634, 1032, 1106, 4951, 5309, 3800,
     5672, 2901, 5439, 1478, 1424, 2777, 5682, 2554, 2117, 2845,
     3867, 2962,  882, 5435, 4174, 4948, 2376, 4987, 3329, 5002]

一组散点数据，为预测模型提供输入。

绘制散点图看一下效果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def show():
    plt.figure(figsize=(10, 6))  # 设置图形大小
    plt.scatter(x, y, alpha=0.5, c='blue', label='实际数据')  # 绘制散点图
    plt.xlabel('月收入（元）')  # x轴标签
    plt.ylabel('月网购支出（元）')  # y轴标签
    plt.title('月收入与网购支出关系散点图')  # 图表标题
    plt.grid(True)  # 添加网格
    plt.legend()  # 显示图例

    # 添加回归线
    #x_line = np.array([min(x), max(x)])
    #y_line = a * x_line + b
    #plt.plot(x_line, y_line, 'r-', label='回归线')
    //回归线 a,b 参数的值这里没有确定

    plt.show()  # 显示图形

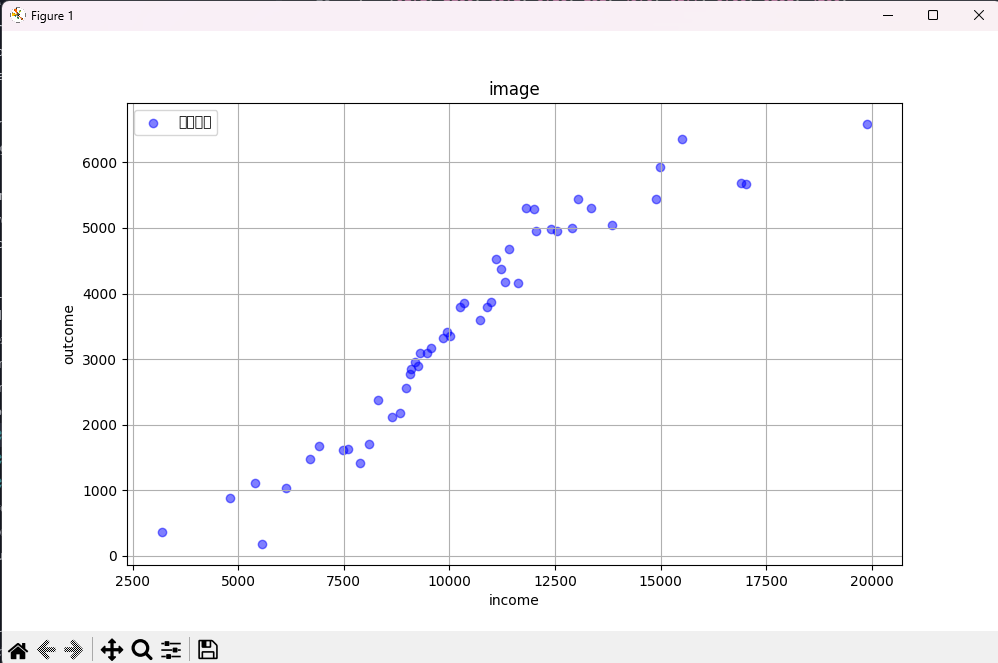
image-20250403220217519

可以看到，x,y 成线性相关

同时，利用 numpy 计算一下 x,y 的相关系数

print(np.corrcoef(x, y))

==》

1
2
[[1.         0.94862936]
 [0.94862936 1.        ]]

相关系数 0.94862936 (接近 -1 或者 1 为强相关)

KNN算法预测

- 使用 heapq.nsmallest 找出k个最接近的收入值

- 计算这k个收入值对应的支出的平均值作为预测结果

大白话：就是给一个 X_ 收入，找出距离 X_ 最近的 K 个数 x，取这 K 个数对应 y 值的平均值作为 X_ 的 Y_ 的预测结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
sample_data = {key:value for key,value in zip(x,y)}
def predict_by_knn(history_data, param_in, k=5):
    """用kNN算法做预测
    :param history_data: 历史数据
    :param param_in: 模型的输入
    :param k: 邻居数量（默认值为5）
    :return: 模型的输出（预测值）
    """
    neighbors = heapq.nsmallest(k, history_data, key=lambda x: (x - param_in) ** 2)		//求最近的x
    return statistics.mean([history_data[neighbor] for neighbor in neighbors])			//求平均值y_

incomes  = [1800, 3500, 5200, 6600, 13400, 17800, 20000, 30000]
for income in incomes:
    print(f"月收入：{income:>5d},月网购支出：{predict_by_knn(sample_data, income):>6.1f}")

运行效果

1
2
3
4
5
6
7
8
月收入： 1800,月支出： 712.6
月收入： 3500,月支出： 712.6
月收入： 5200,月支出： 936.0
月收入： 6600,月支出：1487.0
月收入：13400,月支出：5148.6
月收入：17800,月支出：6044.4
月收入：20000,月支出：6044.4
月收入：30000,月支出：6044.4

可以看到，预测结果简直一坨

原因是这种根据距离求平均值的算法误差太大？

楞猜法预测

由于已知该数据呈一定的线性关系，所以可以根据直线 y=ax + b 去拟合

而参数 a，b 就是我们需要找到的值

问题转化如何找到 a，b,使拟合效果最好

于是定义损失函数求均方误差，就是高中学的方差的平均值

先定义一个很大的 current_loss，然后随机取 a,b，带入 X_ ，将求出的平均方差与 current_loss 比较，若平均方差较小，则更新 current_loss ，继续随机取 a,b ，直到找到使 current_loss 最小的 a,b ，即为所求参数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def get_loss(X_,Y_,a_,b_):
    """损失函数
    :param X_: 回归模型的自变量
    :param y_: 回归模型的因变量
    :param a_: 回归模型的斜率
    :param b_: 回归模型的截距
    :return: MSE（均方误差）
    """
    y_hat = [a_ * x + b_ for x in X_]
    return statistics.mean((v1 -v1)**2 for v1,v2 in zip(y_hat,Y_))
    
# 先将最小损失定义为一个很大的值
min_loss, a, b = 1e12, 0, 0
# 目标是找到一组 a,b 使损失函数最小

for i in range(10000):
        _a, _b = random.random(), random.random() * 4000 - 2000
        loss = get_loss(x, y, _a, _b)
        if loss < min_loss:
            min_loss, a, b = loss, _a, _b
            # 损失值不断减小，a,b 值不断更新并记录
        pbar.update(1)
print(f"最小损失为：{min_loss:.2f}, 对应的斜率为：{a:.2f}, 对应的截距为：{b:.2f}")

incomes  = [1800, 3500, 5200, 6600, 13400, 17800, 20000, 30000]
for income in incomes:
    print(f"月收入：{income:>5d},月网购支出：{(lambda x:a*x + b)(income):>6.1f}")

==》

1
2
3
4
5
6
7
8
9
最小损失为：0.00, 对应的斜率为：0.42, 对应的截距为：-9.39
月收入： 1800,月网购支出： 741.7
月收入： 3500,月网购支出：1451.1
月收入： 5200,月网购支出：2160.5
月收入： 6600,月网购支出：2744.7
月收入：13400,月网购支出：5582.2
月收入：17800,月网购支出：7418.3
月收入：20000,月网购支出：8336.3
月收入：30000,月网购支出：12509.2

效果一般

增大随机模拟次数，加上进度条动态展示模拟进度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
min_loss, a, b = 1e12, 0, 0
# 目标是找到一组 a,b 使损失函数最小

total_iterations = 10000000			//更多次随机模拟
with tqdm(total=total_iterations, desc="训练进度") as pbar:
    for i in range(total_iterations):
        _a, _b = random.random(), random.random() * 4000 - 2000
        loss = get_loss(x, y, _a, _b)
        if loss < min_loss:
            min_loss, a, b = loss, _a, _b
            # 损失值不断减小，a,b 值不断更新并记录
        pbar.update(1)
print(f"最小损失为：{min_loss:.2f}, 对应的斜率为：{a:.2f}, 对应的截距为：{b:.2f}")
incomes  = [1800, 3500, 5200, 6600, 13400, 17800, 20000, 30000]

for income in incomes:
    print(f"月收入：{income:>5d},月网购支出：{(lambda x:a*x + b)(income):>6.1f}")
1
2
3
4
5
6
7
8
9
10
训练进度: 100%|███████████████████████████| 100000000/100000000 [25:49<00:00, 64552.47it/s]
最小损失为：0.00, 对应的斜率为：0.74, 对应的截距为：-196.56
月收入： 1800,月网购支出：1128.8
月收入： 3500,月网购支出：2380.6
月收入： 5200,月网购支出：3632.3
月收入： 6600,月网购支出：4663.2
月收入：13400,月网购支出：9670.2
月收入：17800,月网购支出：12910.0
月收入：20000,月网购支出：14529.9
月收入：30000,月网购支出：21893.1

可见，随着模拟次数的增加，current_loss 越小，a,b 的取值越准确

最后，我们根据这个 a,b 值，来重新画出回归线

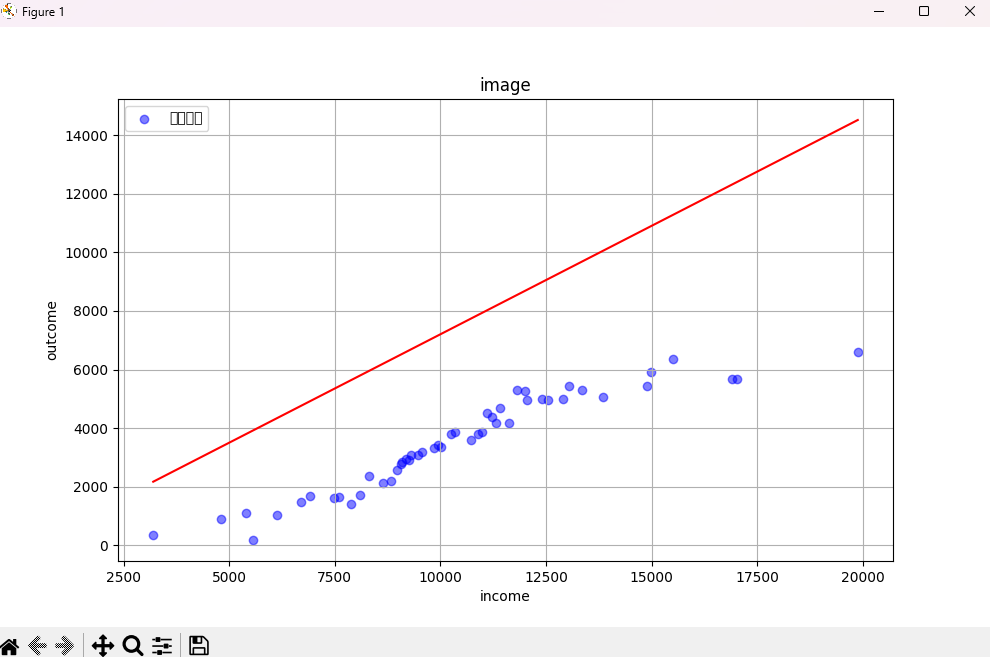
image-20250403222447698

仍然拟合地一坨，后续再进行优化。

后记：初探人工智障，菜鸡一枚。